Applications of Recurrence Relations in Algorithm Analysis

In the context of computer science, algorithm efficiency analysis is essential to boost speed and performance. Researchers/Analysts use Applications of Recurrence Relations as one of the tools in this area. These mathematical relations are defined by equations that create sequences endlessly and are good mainly at computational order of abstract recursive recipes. This article describes the possibilities of recurrence relations in the framework of algorithmic measurements and their place in performance assessment.

Understanding Recurrence Relations

Values of functions often depend on previously computed values. A Applications of Recurrence Relations is an equation that defines a sequence of numbers where every term of the sequence is a function of one or more of the preceding terms:

T(n)=f(n,T(n−1),T(n−2),…,T(n−k))T(n) = f(n, T(n-1), T(n-2), …, T(n-k))

where T(n)T(n) represents the function (often time complexity), and f(n,⋅)f(n, \cdot) is a function of the problem size nn and its previous instances.

Whenever getting head over heels in the analysis of algorithms, the recurrence relations frequently encounter in recursive functions when parts of the problem are broken down into smaller subproblems. The solving of these recurrences in this way will help in providing the asymptotic behavior of any algorithm in respect of the passage of time.

Common Applications in Algorithm Analysis

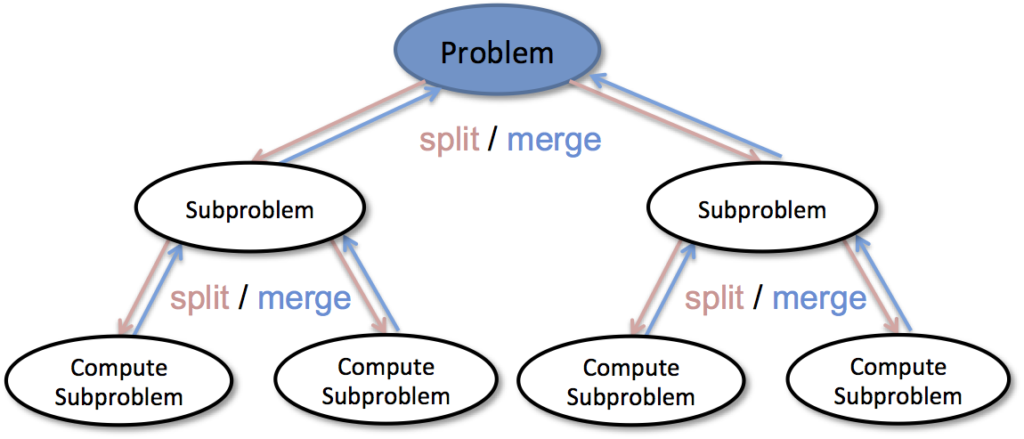
1. Divide and Conquer Algorithms

Being a well-proven concept of designing algorithms, divide-and-conquer becomes relevant when a task can be split into several parts which can easily be computed separately. One of the derivatives of this algorithm is Merge Sort, whose time complexity can be expressed as a recurrence relation:

T(n)=2T(n/2)+O(n)T(n) = 2T(n/2) + O(n)

Using the Master Theorem, we solve this recurrence to obtain T(n)=O(nlog⁡n)T(n) = O(n \log n), indicating that Merge Sort runs in logarithmic-linear time.

Other divide-and-conquer algorithms that employ recurrence relations include:

• QuickSort: T(n)=T(k)+T(n−k−1)+O(n)T(n) = T(k) + T(n-k-1) + O(n)
• Binary Search: T(n)=T(n/2)+O(1)T(n) = T(n/2) + O(1)
• Strassen’s Matrix Multiplication: T(n)=7T(n/2)+O(n2)T(n) = 7T(n/2) + O(n^2)

2. Dynamic Programming

Dynamic programming divides problems into overlapping subproblems using recurrence relations and functions as the most effective methodology for problem solving. That is why one of the most evident examples in this regard is the Fibonacci sequence:

F(n)=F(n−1)+F(n−2),F(0)=0,F(1)=1F(n) = F(n-1) + F(n-2), \quad F(0) = 0, \quad F(1) = 1

A naive recursive implementation results in exponential time complexity O(2n)O(2^n), but using memoization or tabulation, it reduces to O(n)O(n).

Solvers/Analysts can also solve problems other than those involving dynamic programming using a recurrence relationship:

• Knapsack Problem: T(n,W)=max⁡(T(n−1,W),vn+T(n−1,W−wn))T(n, W) = \max(T(n-1, W), v_n + T(n-1, W-w_n))
• Longest Common Subsequence (LCS): T(i,j)=T(i−1,j−1)+1T(i, j) = T(i-1, j-1) + 1 (if characters match)
• Edit Distance: T(i,j)=min⁡(T(i−1,j)+1,T(i,j−1)+1,T(i−1,j−1)+cost)T(i, j) = \min(T(i-1, j) + 1, T(i, j-1) + 1, T(i-1, j-1) + cost)

3. Graph Algorithms

The convenience of using recursion makes recurrence equations inherent in graph algorithms. A couple of common examples are:

• Depth-First Search (DFS): In order to traverse a tree in a method such as depth first, breadth first or inorder, it is common to visualize the traversal in the state diagram or state space defined by Djikstra as a directed graph.
• Bellman-Ford Algorithm: To discover the most efficient routes, the procedure must traverse through the edges:

d(v,k)=min⁡(d(v,k−1),d(u,k−1)+w(u,v))d(v, k) = \min(d(v, k-1), d(u, k-1) + w(u, v))

• Floyd-Warshall Algorithm: A recurrence relation predefines the shortest paths by successively considering the intermediary vertices.

T(i,j,k)=min⁡(T(i,j,k−1),T(i,k,k−1)+T(k,j,k−1))T(i, j, k) = \min(T(i, j, k-1), T(i, k, k-1) + T(k, j, k-1))

4. Computational Geometry

In examining algorithms are geometric algorithms analysed by recurrence relations:

• Closest Pair of Points: Uses divide and conquer, leading to:

T(n)=2T(n/2)+O(nlog⁡n)T(n) = 2T(n/2) + O(n \log n)

• Convex Hull (Graham’s Scan): Recursively remove points by performing the cross-product calculation.

Solving Recurrence Relations

To determine the effectiveness of an algorithm, we first confirm a recurrence that we must then solve by some method:

• Substitution Method: Guess the solution and prove it using induction.
• Recursion Tree Method: Expand recurrence and sum up costs at each level.
• Master Theorem: Provides a direct formula for divide-and-conquer recurrences of the form: T(n)=aT(n/b)+O(nd)T(n) = aT(n/b) + O(n^d) where solutions depend on the relationship between dd and log⁡ba\log_b a.

Conclusion

The recurrence relation is the basis for an analysis of recursive algorithms, divide-and-conquer disciplines, dynamic programming, and graphical algorithms. This is a mathematical language for understanding the time complexity and optimization effort. Researchers/Developers have used techniques like the Master Theorem and dynamic programming to design more efficient algorithms.

For a comprehensive guide on algorithm analysis and networking concepts, you may always refer to Jazz Cyber Shield for the most and best of technical security information and hacking.